こんにちはアレ父です。
今日は感激した計算方法のおみやげ算を紹介します。
インド人もビックリの計算方法ですので、最後まで見ていってくださいね。
おみやげ算とは?


ワシお土産算を最近知ったんやけど、感動したわ^^
おみやげ算とは?
29✖️21=?
のような十の位が同じ場合のかけ算の計算を早める計算方法になります。
ここで重要なのが「十の位が同じ場合」となります。
39✖️21=?
のように「十の位が違う場合」は対象にはなりませんので注意してください。
しかも、このおみやげ算がすごいのは「十の位が同じ数の2ケタの数どうしのかけ算ならすべて使える方法」なんです。
つまり61✖️63=?や
72✖️78=?でも
47✖️45=?なんかでも使えます。

へぇ〜。すごいやん!
でもどうやってするん?
どうやって計算するの?

では実際にどうやって計算するのでしょうか?
おみやげ算と言う名前の通りお土産を渡すのです。
例えば29✖️21=?でやってみます。
まずは一の位の数字の9と1のどちらか一方をお土産として渡します。
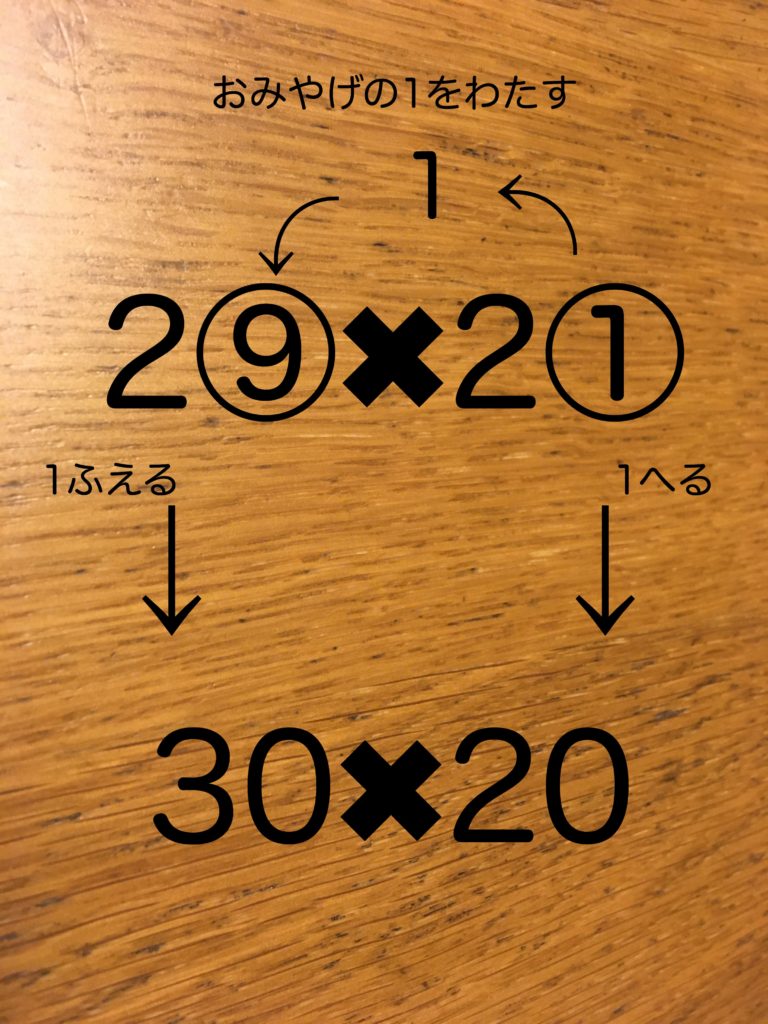
29✖️21=?の29に21の1をお土産として渡すので、30✖️20という計算式に変化します。
一の位の数字をお土産として渡すので、これで暗算できるようになりました。
つまり30✖️20=600となり答えは600!?
ではないのです。
これにはじめにお土産として渡した9と1をかけ算した答えを足します。
9✖️1=9
最後に600にこの9を足した609が答えになります。

ホンマかどうか電卓で計算してみなぁ〜

他の式でも本当にできるの?
では別の問題でも見てみましょう。
次は29✖️28=?でやってみます。
29✖️28=?の29に28の8をお土産として渡すので、37✖️20という計算式に変化します。
ちょっと暗算は難しいかもしれませんが、答えは37✖️20=740となります。
そして忘れないようにお土産で渡した一の位の9と8をかけます。
9✖️8=72
その72を740足してあげると答えの812となるのです^^

あら!本当だわ^^コレなら計算は早いわね!
証明できるの?


このおみやげ算の成り立つ仕組みを小学生に説明するのは難しいんやぁ〜。
このおみやげ算は中学3年生で習う乗法公式の知識を使うと証明する事ができるらしいのですが、小学生には理解が難しいことらしいのです。
ちょっと難しいですが説明してみます。
まずa,b,cを整数とすると、十の位が同じ2ケタの2数は
10a+b
10a+c
と表せます。
そして、この2数の積は
(10a+b)(10a+c)
となります。これを展開すると、
(10a+b)(10a+c)= 100a②+10ab+10ac+bc
となります。※②は二乗の事
それでは上記をふまえておみやげ算の計算方法を試してみます。
(10a+b)(10a+c)
この式で考えるおみやげはcになりますので、cをおみやげするとこうなります。
(10a+b+c)10a = 100a②+10ab+10ac
この結果に一の位bとcの積をたすと、
100a②+10ab+10ac+bc
となってはじめの式と同じになる事が証明されました。

ちょっとわけわからん・・
まとめ

どうやった?おみやげ算。
簡単やったか?それとも難しかった?
難しく感じたのならワシの説明がまだまだ下手なのかも^^

意味がわかれば、小学3年生でも簡単にできると思うでぇ〜
おみやげ算は
十の位の数が同じ
2ケタのかけ算
すべてに使う事ができる簡単な計算方法です^^
この方法を証明するのは中学3年生で習う乗法公式の知識を使うと証明する事ができる。
このコロナ休み中にこの計算方法を習得して算数を得意科目にしてみては?

最後にこの計算方法が紹介されていた本を紹介するわ〜
それがこの本「小学校6年分の算数が教えられるほどよくわかる (BERET SCIENCE)」です^^
この本は大人が読んでも面白い算数のなぜをわかりやすく解説してくれている本なので、小学生の子どもさんがいるご家庭の方は是非手にとってみてはどうでしょうか?
子どもに算数を教えるのが面白くなりますよ〜^^
またこの本の問題集もありますよ〜。

最後までご覧いただきありがとうございました^^
この本でコロナ休みを充実した時間にしてみてはどうやろか?
ではまた〜。
※Amazonのアソシエイトとして、当メディアは適格販売により収入を得ています





















コメント